行测备考:浅析植树问题与方阵问题
数量关系的趣味杂题中,包含了植树问题、方阵问题等,有些题型除了本身的公式考查,题型变化也比较多,需要掌握重点公式。
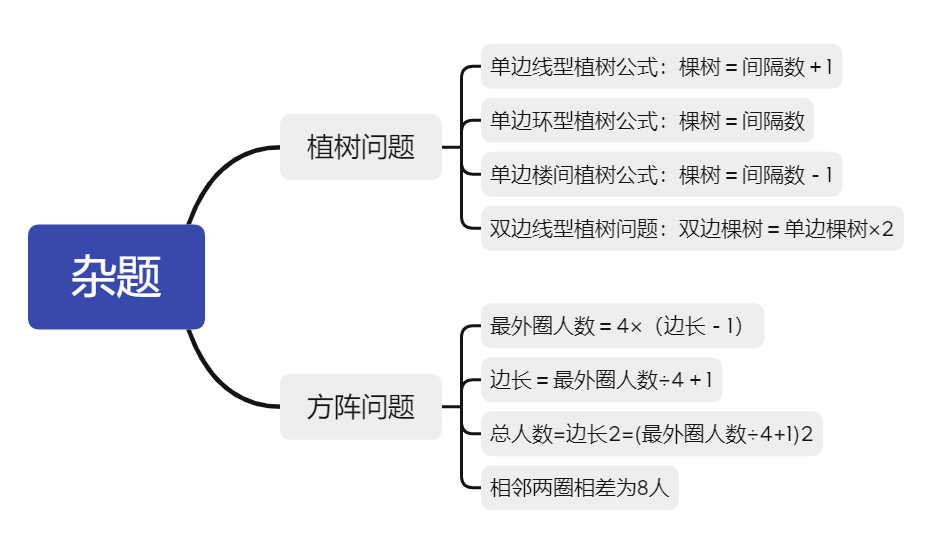
一、植树基本公式
①单边线型植树公式:棵树=间隔数+1
②单边环型植树公式:棵树=间隔数
③单边楼间植树公式:棵树=间隔数-1
④双边线型植树问题:双边棵树=单边棵树×2
二、公式应用
【例1】807路公交车一共有20个公交站点,从第一站国贸到第二站八里桥有11公里,余下每两个公交站点之间的距离都是500米,那么这条公交线路的距离总和是()公里。
A.19 B.19.5
C. 20 D.20.5
【答案】C
【解析】第一步,本题考查的植树问题。
第二步,从第一个站点到第二十个站点中间有19个间隔,第一个间隔长为11公里,剩余间隔总长为18×500=9000米=9公里,所以这条公交线路的距离总和=11+9=20公里。
因此,选择C选项。
【例2】某小区两栋楼之间间距为375米,现在要在两栋楼之间均匀种74棵树,请问第5棵树到第26棵树之间的距离是()米。
A.90 B.95
C.100 D.105
【答案】D
【解析】
第一步,本题考查植树问题。
第二步,两栋楼之间均匀种74棵树会产生75个均匀间隔,于是每个间隔为375÷75=5(米)。而第5棵树到第26棵树之间有26-5=21(个)间隔,因此距离为5×21=105(米)。因此,选择D选项。
三、方阵问题基本公式
①最外圈人数=4×(边长-1)
②边长=最外圈人数÷4+1
③总人数=边长2=(最外圈人数÷4+1)2
④相邻两圈相差为8人
四、公式应用
【例3】体育馆有一块正方形草坪,若沿草坪四周每隔2米插一面彩旗,正好插上16面彩旗。则这块草坪的面积为()平方米。
A.40 B.48
C.56 D.64
【答案】D
【解析】第一步,本题考查端点类问题,属于植树问题。
第二步,根据单侧环形植树:棵数=总长÷间隔,总长=棵数×间隔;因此该正方形草坪周长=16×2=32(米),正方形边长为8米。
第三步,则这块草坪的面积为8×8=64(平方米)。
因此,选择D选项。
【例4】某单位参加团体操比赛,根据队形的需要,摆成一个三层空心方阵。如果外层每边站立15个人,则摆成这个方阵最里层一圈共需要多少人?
A.30 B.40
C.50 D.60
【答案】B
【解析】
第一步,本题考查端点类问题,属于方阵问题。
第二步,由外层每边站立15个人,根据方阵最外层总个数=(n-1)×4,则最外层有(15-1)×4=56(人);由方阵外一层总个数比内一层的总个数多8,得最里层为56-8×2=40(人)。
因此,选择B 选项。
通过上面讲述,相信各位考生对植树问题和方阵的考法有了系统的了解,在了解之后还仍然需要做大量的习题练习进行巩固,这样方能在考试中一举攻破这个考点。