概率问题是国考，联考数量关系基本题型，也是常考题型之一。近三年，国考均考查了概率问题，15,17年联考也涉及此类题型。因此概率问题需要大家重点掌握。概率问题有其本身固有的特点，对于特定的概率问题可以秒杀解题。

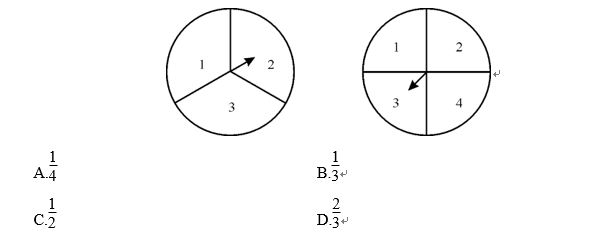
　　【例1】某商场为招揽顾客，推出转盘抽奖活动。如下图所示，两个数字转盘上的指针都可以转动，且可以保证指针转到盘面上的任一数字的机会都是相等的。顾客只要同时转动两个转盘，当盘面停下后，指针所指的数相乘为奇数即可以获得商场提供的奖品，则顾客获奖的概率是( )

　　

 

　　【答案】B

　　【解析】本题考查的是分步概率。相乘为奇数的情况即两个转盘均为奇数的情况。第一个转盘转到奇数的概率为，第二个转盘转到奇数的概率为，则两盘都转到奇数的概率为×=，故正确答案选B。

　　秒杀计：对于顾客而言要么获奖要么不获奖，这两个事件的概率加起来为1，而B,D选项加起来恰好为1，所以正确选项极有可能是B,D其中之一。依据常识获奖的概率应该偏小(否者商家亏本)，故选B。

　　秒杀技巧：一个事件的概率和它对立事件的概率和必然为1，因此我们在求解概率问题时，如果某两个选项的和为1，则正确选项极有可能是两者之一。

　　【例2】两支篮球队打一个系列赛，三场两胜制，第一场和第三场在甲队的主场，第二场在乙队的主场。已知甲队主场赢球概率为0.7，客场赢球概率为0.5。问甲队赢得这个系列赛的概率为多少( )

　　A.0.3 B.0.595

　　C.0.7 D.0.795?

　　【答案】C

　　【解析】本题是分类概率问题。分情况讨论，甲队赢得系列赛的情况为：甲甲、甲乙甲、乙甲甲，相应概率分别为:0.7×0.5，0.7×0.5×0.7，0.3×0.5×0.7，相加即得甲队赢得这个系列赛的概率为0.7。故答案选择C。

　　本题分类讨论对部分同学有一定的难度，秒杀计可快速解题。

　　秒杀计：对于甲而言要么获胜要么输球，这两个事件的概率加起来为1，而A,C选项加起来恰好为1，所以正确选项极有可能是A,C其中之一。由题知甲每场比赛获胜的概率都不低于0.5，故三局两胜获胜概率也不会低于0.5，排除A。故本题选C。

　　【例3】一辆公交车从甲地开往乙地需经过三个红绿灯路口，在这三个路口遇到红灯的概率分别是0.4、0.5、0.6，则该车从甲地开往乙地遇到红灯的概率是( )

　　A.0.12 B.0.50

　　C.0.88 D.0.89

　　【答案】C

　　【解析】本题考查的是分类概率。从正面入手非常复杂，所以从其对立面(反面)入手。对立面：没有遇到红灯，即三个路口都没有遇到红灯。对立面概率为：(1-0.4)*(1-0.5)*(1-0.6)=0.12，所以遇到红灯的概率为：1-0.12=0.88。因此，答案选择C选项。

　　秒杀计：该车从甲地开往乙地要么遇到红灯要么没有遇到红灯。这两个事件的概率加起来为1，而A,C选项加起来恰好为1，所以正确选项极有可能是A,C其中之一。结合选项发现C,D两项的答案非常接近，依据选项的亲密原则，所以C,D其中之一可能是正确选项。两者相结合选C。

　　总结：1、在计算概率问题时，如果某两个选项的和为1，则正确选项极有可能是两者之一(选项的相关性)。结合题意，选项(如选项的亲密性)或常识往往能得出正确选项。

　　2、计算概率时，如果从正面入手比较困难，可以从事件的对立面(反面)入手，求出对立事件(反面事件)的概率，进而得出所求事件的概率。

　　更多公务员备考关注浙江华图微信公众号(zhejianght)，招考信息、考试资料等精彩内容每日推送。