2023行测备考技巧：如何更好的理解和记忆对当关系

　　对当关系 ， 指的是具有相同素材的命题之间的真假制约关系， 在我们做题的过程中常常表现为以下这几个命题之间存在的矛盾关系、反对关系，而通过题目中给出的矛盾关系和反对关系，我们就可以进行“真假定位”，从而确定真命题或者假命题的一个范围被限定在了题目中所给的哪几句话当中。比如下面这题：

　　例题1： 某省游泳队进行了为期一个月的高原集训，集训最后一日所有队员进行了一次队内测试，几位教练预测了一下队员的成绩：

　　张教练说：这次集训时间短，没人会达标。

　　孙教练说：有队员会达标。

　　王教练说：省运会冠军或国家队队员可达标。

　　测试结束后，只有一位教练的预测是正确的。

　　由此可以推出：

　　A.没有人达标

　　B.全队都达标了

　　C.国家队队员未达标

　　D.省运会冠军达标

　　有过做题经验的小伙伴应该就可以知道，一位教练说没有队员会达标，另一个教练说有队员会达标，我们就可以判断出这两个教练必定有一个人说的是真话，有一个人说的是假话。这体现出来的就是“所有都”和“有的不”这两个命题之间的必有一真必有一假的真假制约关系。我们在做题中重要运用到的几个关系分别为以下几个基本性质命题之间的关系：

　　1、所有的A都是B

　　2、所有的A都不是B

　　3、有的A是B

　　4、有的A不是B

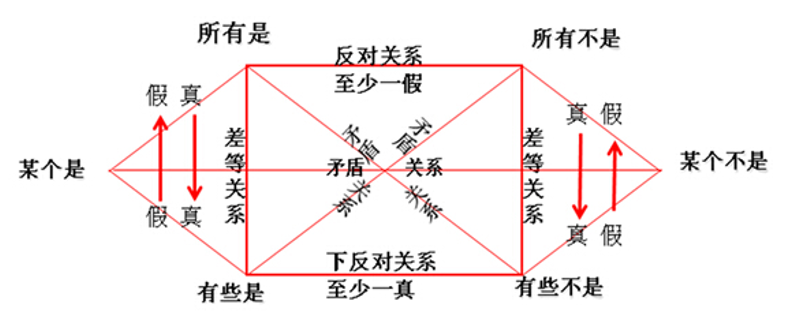
　　当然，如果只是为了刚刚初学的时候方便做题，直接把上面给的这个图记下来，多加练习并且熟练的运用就可以了，但是知其然还要知其所以然才能记得更扎实，以防脑子突然短路卡壳，毕竟一道简单题目没做出来也会影响后续的做题心态，所以现在提供一种方法让各位考生更好的理解对当关系。

　　方法一：运用集合推理的思维进行理解

　　首先我们要知道，两个集合之间到底可能存在几种情况，这个我们通过一个图来方便大家理解：

　　可以发现，A和B这两个集合从毫无相干到完全重合，一共也就这5种情况，没有第6种了，带着这个前提我们继续去思考：这四个基本性质命题该如何用集合来表示出来呢?

　　上述四个基本性质命题在集合中分别可以这样表示：

　　将集合表示出来后，其实对当关系的原理我们就找到了，比如说，为什么说“所有都”和“有的不”是一组矛盾关系呢?矛盾关系我们都知道，两者必定一真一假，而且没有第三种情况的存在。而我们看到，“所有A都不是B”和“有的A是B”这两个命题所属的集合中，并没有相同的情况，只要是属于其中一个命题的集合，就必定不属于另一个命题，同时，这两个命题已经穷尽了A和B的所有集合情况(前文分析过是5种)，所以满足矛盾关系的定义，必有一真一假且没有第三种情况。同理，“所有A都是B”和“有的A不是B”也是相互没有交叉相同的集合存在，也共同构成了所有集合情况，因此也是一组矛盾关系。

　　用这几个集合还可以把上反对关系和下反对关系的原理给表示出来。反对关系的和矛盾关系的不同点在于，是存在同真同假的第三种情况的，那为什么说上反对关系中必有一假，可以同假，而下反对关系汇总必有一真，而且可以同真呢?我们还是结合这几个集合来看。首先说上反对关系“所有A都是B”和“ 所有的A都不是B ”，两个命题所属集合部分没有相同的，所以A和B两集合的实际情况不可能同时满足这两个命题，最多只能满足其中一个，而且可以两个都不满足，因为“所有A都是B”和“ 所有的A都不是B ”加起来只有3个集合，还有2种情况没有被包含进来，因此存在第三种情况也就是“同时为假”。

　　对于下反对关系“ 有的A是B ”和“ 有的A不是B ”也是如此，两个命题已经包含了所有的可能性，不可能同时为假，所以必有一真，而且存在同时为真的这一种情况(如两集合交叉的情况)。

　　从集合推理出发，除了能让我们理解矛盾关系和反对关系，还可以有助于我们学习命题之间的换位关系，如有的A是B和有的A不是B，所有A都是B和所有B都是A等等命题之间的相互转换，这个留在下一期再和大家分享，不过相信掌握了“画集合”这一个思想后，各位考生也一定可以自己画出来并找到换位关系中的原理的，大家加油!