2021年浙江公务员考试行测技巧:青蛙跳井

　　在往年国家公务员考试行测考试数学运算中，青蛙跳井问题可能是困扰考生的难题，青蛙跳井问题灵活多变增加了题目难度。下面小编结合具体的例子给大家讲解基本青蛙跳井问题。希望对各位考生的2017国家公务员行测考试有所帮助。

　　基本青蛙跳井问题

　　我们先由一道简单的例题认识一下青蛙跳井问题。

　　【例题】现有一口高10米的井，有一只青蛙坐落于井底，青蛙每次跳的高度为5米，由于井壁比较光滑，青蛙每跳5米下滑3米，这只青蛙跳几次能跳出此井?

　　A.4

　　B.5

　　C.6

　　D.7

　　【解析】B

　　方法一：枚举法

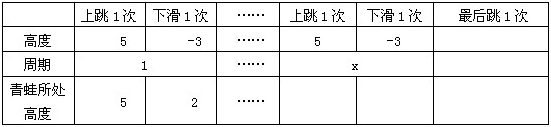
　　此题比较简单，可以通过枚举法快速得到答案，但仅仅用该方法显然不能满足目前考试的需要，因为实际考试中，数据可能会较大，枚举过于耗时，枚举情况过多时也容易马虎出错，所以在此讲述此方法主要是为了便于大家理解青蛙跳井的整个过程。

　　青蛙跳井问题关键特征：周期性、周期内有正有负。

　　我们讲这个例子主要是为了得出针对此类问题，简单但适用性更强的解题方法-不定方程。

　　方法二：不等式法

　　先来分析一下青蛙跳井问题，青蛙不停地上跳下滑，一直在做周期性运动，我们可以把上跳1次下滑1次看做1个周期;不管最终青蛙跳几次才能跳出此井，有一点是确定的，第一次跳出井口的时，它是在上跳的过程中，而不可能是在下滑的过程中，那么扣除最后1次跳出井口，其它恰好是完整周期，当最后一次下滑后，青蛙距离井口的高度≤跳1次能完成的高度时，青蛙再跳1次，即可跳出井口。

　　以此题为例，我们假设青蛙运动x个周期后，再跳1次，即可跳出井口。

　　青蛙每运动1周期能上移2m，运动x个周期后，上移(2x)m，此时距离井口的高度为10-2x≤5，解得x≥2.5，所以x=3，也就是青蛙运动3个周期后，再跳1次，即可跳出井口，与我们前面枚举法做出来的结果相同，但就通过解不等式，就省却了枚举的过程，计算量小，用时短，不易出错。

　　总结一下解题方法：

　　1.找到周期。分析每周期情况：上跳1次下滑1次为1周期，每周期完成高度2m，每周期完成高度的最大值5m。

　　2.解不等式。假设青蛙运动x个周期后，再跳1次，即可跳出井口。运动x个周期后剩余高度=总高度-每周期完成高度×x≤每周期完成高度的最大值，解出周期数。

　　3.计算次数。x个周期所用次数+x个周期后剩余高度所用次数，两部分分别计算相加。

　　再来做一题，练习一下不等式法解决青蛙跳井问题。

　　【例题】现有一口高40米的井，有一只青蛙坐落于井底，青蛙每次跳的高度为4米，由于井壁比较光滑，青蛙每跳4米下滑1米，这只青蛙跳几次能跳出此井?

　　A.11

　　B.12

　　C.13

　　D.14

　　【解析】C

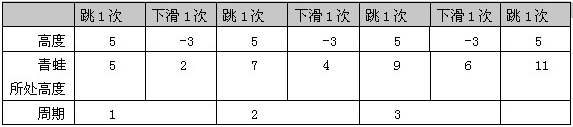
　　1.找到周期。分析每周期情况：上跳1次下滑1次，每周期完成高度3m，每周期完成高度的最大值4m。

　　2.解不等式。假设青蛙运动x个周期后，再跳1次，即可跳出井口。运动x个周期后剩余高度=40-3×x≤4。解出x≥12，所以运动了12个周期。

　　3.计算次数。12个周期所用次数12次+12个周期后剩余高度所用次数1次=13次。